乽偙偺傛偆側偙偲偼巚偄偮偒偵偔偄偺偱偼側偄偐丅乿偲懠偺惗搆偵暦偒傑偡偲丄亀拞妛峑帪戙偵峴偭偰偄偨弇偱偼丄p搙偺栤戣偱暘偐傜側偄偲偒偼丄惓嶰妏宍傗丄擇摍曈嶰妏宍傪昤偄偰傒傞偲傛偄丅乿偲嫵偊傜傟偰偄偨丅亁偲偺偙偲偱偟偨丅
惗搆夝摎丂丂侾擭俁慻俁係斣丂怷丂桾搒丂丂俀侽侽俆擭俋寧
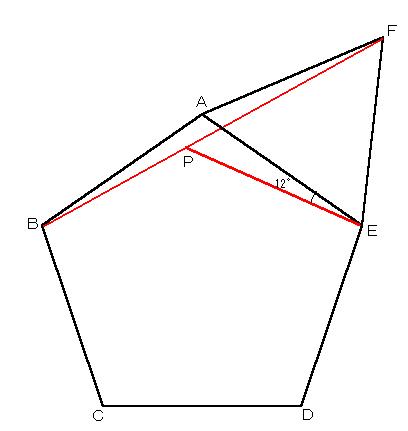
偙偺偲偒丄佢俛俙俤亖108亱側偺偱丄佢俛俙俥亖168亱丅
嶰妏宍俙俛俥偼俙俛亖俙俥偺擇摍曈嶰妏宍偱偁傞偺偱丄佢俙俛俥亖佢俙俥俛亖6亱
傛偭偰丄揰俹偼俛俥忋偵偁傞丅
佢俙俤俹亖12亱偲側傞傛偆偵揰俹傪曈俛俥忋偵庢傟偽丄塃恾偺傛偆偵側傝丄偙偺偲偒丄佢俹俙俠傪媮傔傟偽傛偄丅
佢俹俤俥亖60亱+12亱亖72亱丄佢俤俥俹亖60亱-6亱亖54亱
佢俥俹俤亖180亱-72亱-54亱亖54亱
佢俤俹俥亖佢俤俥俹傛傝丄嶰妏宍俤俥俹偼擇摍曈嶰妏宍
亪丂俤俥亖俤俹丂乧嘆
嶰妏宍俤俥俹偼惓嶰妏宍側偺偱俤俥亖俤俙丂乧嘇
嘆嘇傛傝俤俙亖俤俹
亪丂佢俤俙俹亖乮180亱-12亱乯亐2亖84亱
亪丂佢俛俙俹亖108亱-84亱亖24亱
佢俛俙俠亖乮180亱-108亱乯亐2亖36亱
佢俹俙俠亖佢俛俙俠-佢俛俙俹亖36亱-24亱亖12亱