

本校の数学クラブのメンバーが、6番の解き方についてパワーポイントを使い、1年生全員の前で発表しました。以下に、その発表原稿とパワーポイント画像添付という形で掲載します。
発表原稿
数学クラブです。今回、2011年度日本数学オリンピック予選に、1年
生10人2年生6人が参加しました。出題数は全部で12問。私たちはこの予選を1月9日の成人の日に洛北高校で受けてきました。予選の合格ラインは8問で
した。最高で7問解いた人がいましたが、残念ながら本選に進むことはできませんでした。今日は、その問題の中から第6問を解説していきたいと思います。
〔1〕
では問題です。手元の資料を見てください。簡単に説明すると、
2×100のマス目を赤と青の2色で塗り分けるとき、それが何通りあるかを求めるという問題です。ただし、色の塗り方には2つ条件があって、まず1つ目
は、すべて赤やすべて青はだめだということです。そして2つ目は…〔2〕
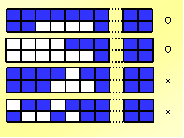
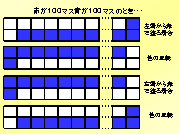
この上から3つ目の図のように、同じ色で塗ったマスが辺を共有していな
いので条件を満たしていません。この図の場合、青が辺を共有していません。これと同様に、この一番下の図は、角を共有していますが辺を共有していないので
条件を満たしません。このように考えると、この上の2つの図が条件に当てはまる正しい図ということになります。〔3〕
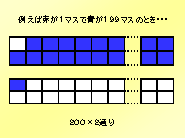
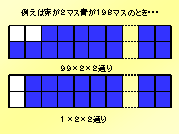
ではまず、赤のマスの数を変えて考えていくことにします。2×100の
200のマス目に、赤を1マス、青を199マス塗ったときを考えました。その場合、この上の図のように表すことが出来ます。この1マスの赤が塗れる箇所
は、条件を考えるまでもなく全てのマスに塗りつぶすことが出来るので全部で200通りあります。また、この下の図というのは同じ要領で青を1マス、赤を
199マス塗ったときです。こちらも、さっきと同じように200通り塗ることが出来ます。ここでまとめると、ある1色を1マス、他の1色を199マス塗る
際には、塗り方が200通り、そして色の反転が赤と青の2通りありますので、このように 200×2通りあります。〔4〕
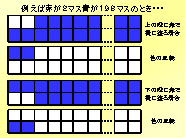
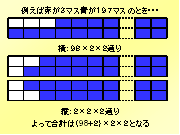
次に、赤を2マス、青を198マス塗ったときを考えました。ここからは、2通りに場合分けして考えることにします。まず1通り目は、上の段に赤を横に2マス塗った場合とその場合における色の反転。また、下の段に赤を横に2マス塗った場合とその色の反転とがあります。〔5〕
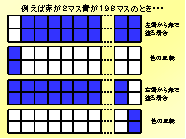
そして2通り目は、左端から赤を縦に塗った場合とその色の反転。また、右端から赤を縦に塗った場合とその色の反転とがあります。〔6〕
つまり、ある1色を2マス、他の1色を198マス塗る場合には、ある1
色を横に塗れる箇所が99通り。そして、横に塗るときの段が上下で変わる2通りと色の反転2通りとがあるので、99×2×2通り。また、ある1色を縦に塗
るとなれば、縦に塗るときの端が左右の2通りあるので、1×2×2通りあるのです。縦に塗る際に端から塗るのには、理由があります。赤のマスだけで出来た
1つの図形と、青のマスだけで出来た1つの図形とが、200のマスの中に1つずつないと、問題文の条件にあてはまらないからです。〔7〕
ちなみに、ここに示している方法で計算すると便利なので、参考にして下さい。〔8〕
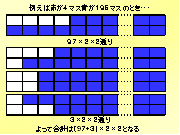
次に、赤を3マス,青を197マスの時は、一段に赤を塗る場合98通り、上と下2段あるので2通り、赤と青2色あるので、式は98×2×2となります。左端に固定した場合赤1マスの塗り方は2通りとなり、赤と青2色、右端の場合があるので式は2×2×2となります。よって合計は(98+2)×2×2となります。〔9〕
次に赤が4マス,青が196マスの時も同様なので、赤を一段に横に塗る場合は97通り、つまり式は97×2×2となります。縦の場合も3通りあるので、式も3×2×2となり合計は同様に(97+3)×2×2となります。〔10〕
ここまでは、1マス・2マス・3マス・4マスとやってきましたが、ここ
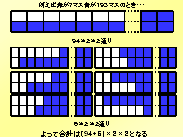
で少し飛ばして、たとえば赤が7マスの場合を考えます。赤が7マス青が193マスのときに、今までと同じように、横で考える場合と縦で考える場合の2つの
場合で考えます。まず横の場合、上の段の100マスに赤の7マスが並ぶのは94通りあって、それの色の反転と上下の反転があるので、このような式になりま
す。次に、縦の場合、端の2マスを固定して考えたときに、残った5マスをどこに置くかと考えると、このスライドに示しているように6通りになります。まと
めると、このような式になり、赤が7マスの場合はこのような式になります。〔11〕
これ以降も、次の8マス、9マスと、縦と横の2通りに分けて考えるとよ
いのですが、最後の100マスと100マス、つまり赤が100マスで青が100マスのときだけ、少し特別な場合になります。といいますのは、このスライド
のように、色の反転、左右の反転、その色の反転、という風に4通り出来るのですが、この1番上と1番下、2番目と3番目は同じになります。ということは、
これは4通りではなくて実は2通りなのです。〔12〕
ということで、100マスのときの式は100×2ということが分かります。そうしますと、1マスから100マスまで全部式が出てきたので、次の人に今までの場合分けをおさらいしてもらいます。〔13〕
では、ここまでの場合分けを1枚のスライドにまとめるとこうなります。
皆さん、もうお気付きですね。こうやって縦に並べると一目瞭然だと思います。1マスと199マスの場合は200×2の400通り、2マスと198マスの時
は(99+1)×2×2つまり100×4の400通り、3マスと197マスの時も(98+2)×2×2の400通り、つまり1マスから99マスまで塗る場
合は全て400通りずつとなっています。ただ、100マスと100マスの時だけ、先程の説明のように色の反転と左右上下の逆が同じものになるので、
(1+99)×2つまり100×2となり200通りになることに注意が必要です。ちなみに、これまでの場合分けの際に、すでにそれぞれの場合について色の
反転と左右上下の逆を考えているので、ここでは101マス以降の場合について、考える必要がありません。この問題ではこれら全ての合計を求めよ、というこ
とだったので、答えは400×99+200よって39800通りということになります。〔14〕
皆さん、いかがでしたか?今日の私たちの発表を聞いて、少しでも数学オ
リンピックに興味を持っていただければ幸いです。また、ここに示したものは、この問題の解法のうちのたった一つです。他にもたくさんの解き方があります。
実際、私たちの間でも幾つかの解き方が提案されました。気になる人は家に帰ってからでも探してみてください。きっと見付かると思います。では、ご静聴あり
がとうございました。〔15〕
パワーポイント
〔1〕 〔2〕 〔3〕


〔4〕 〔5〕 〔6〕
〔7〕 〔8〕 〔9〕

〔10〕 〔11〕 〔12〕
〔13〕 〔14〕 〔15〕


