２００７年数学オリンピック国内予選問題４　　２００７年１月８日　　１年１組２３番　津山　竣太郎

問題

は十の位がでない桁の正の整数であり、の上桁と下桁をそれぞれ桁の整数と考えたとき、この数の積はの約数となる。そのようなをすべて求めよ。

解答

  (は２桁の整数)

問題文よりはの倍数なので

と表せる(は整数)

ここで、この式を因数分解します。

しかし、このままでは因数分解できないので、両辺にmをかけます

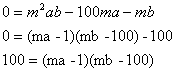
はそれぞれ整数で、

なので、

の組み合わせは、

しかし、は桁なので、

よって、は不適

この通りの中から解答を考えます

の場合

ならで３桁なので不適

ならで１桁なので不適

の場合

ならで３桁なので不適

ならで１桁なので不適

ならで１桁なので不適

ならで１桁なので不適

の場合

ならで３桁なので不適

なら，となり条件を満たす

ならで１桁なので不適

ならで１桁なので不適

の場合

ならで３桁なので不適

なら，となり条件を満たす

ならで１桁なので不適

ならで１桁なので不適

の場合

ならで３桁なので不適

ならで１桁なので不適

以上から、