２００６年数学オリンピック国内予選問題９　　　２００６年６月１２日　　　２年４組　森田　好美

問題

，，である三角形の内部に点をとる。三角形の外接円，三角形の外接円，三角形の外接円の半径がすべて等しいとき、その等しい半径を求めよ。

解答

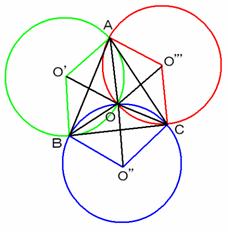
　の外接円の中心を，の外接円の中心を，の外接円の中心をとし、

　，，

，，

，

　とおくと、

　

　円，円，円は半径が等しいので、

扇形と扇形と扇形を合わせると円ができる。

　したがって、の外接円の半径を求めればよい。

　余弦定理より，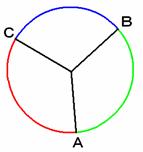　

相互関係から，　

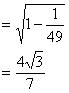
正弦定理より，
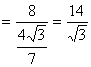