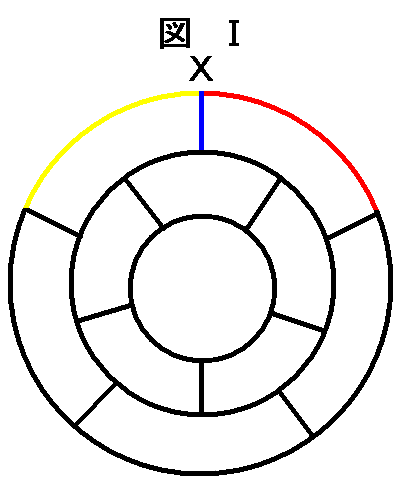
丂傛偭偰丄恾嘦偱倃偐傜惵愒偲恑傫偩屻偺宱楬傪俇攞偡傟偽傛偄偙偲偵側傞丅
丂傑偨丄惵愒偲恑傫偩傜丄墿怓偺慄偼捠傞偙偲偑弌棃側偄丅傛偭偰丄椢偺慄傪捠傜偹偽側傜側偄偙偲偵側傞丅
惓廫擇柺懱偺傂偲偮偺捀揰倃傪偲傞丅堦旵偺傾儕偑倃傪弌敪偟丄惓廫擇柺懱偺曈忋偺傒傪曕偒丄倃埲奜偺偡傋偰偺捀揰傪偪傚偆偳侾搙偢偮捠夁偟偰丄倃偵栠偭偰偒偨丅傾儕偺曕偄偨宱楬偲偟偰峫偊傜傟傞傕偺偼壗捠傝偁傞偐丅偨偩偟丄夞揮偱廳側傝崌偆傛偆側宱楬傗丄摴弴偑媡偵側偭偨偩偗偺宱楬傕丄堎側傞傕偺偲偟偰悢偊傞丅
| 丂惓廫擇柺懱偺傂偲偮偺柺偵寠傪奐偗丄峀偘偰暯柺忬偵偡傋偰偺柺傪墴偟晅偗傞丅偦偺嵺丄奺柺偺宍偼偙偺栤戣傪峫偊傞偵嵺偟偰娭學側偄偺偱丄塃恾嘥偺傛偆偱偁傞偲偟偰傕傛偄丅偨偩偟丄尦乆偺惓廫擇柺懱偺懳徧惈偐傜峫偊偰丄倃傪弌敪偟偨屻丄愒丄惵丄墿偺偄偢傟偵恑傓偵偟偰傕丄偦偺屻偺宱楬偺屄悢偼摨偠偱偁傞偲峫偊傜傟傞丅傛偭偰丄惵偺曽岦偵恑傫偩屻偺宱楬傪丄3攞偡傟偽傛偄丅 |  |
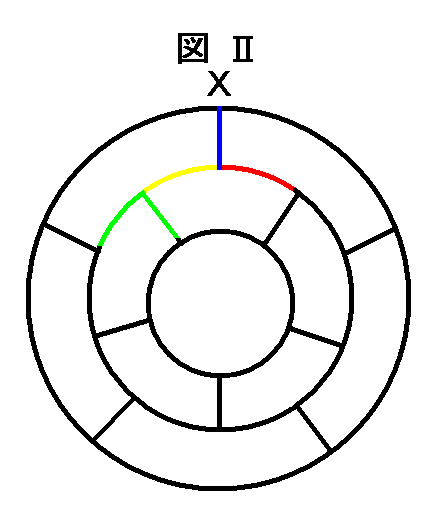
| 丂恾嘥偱惵偺曽岦偵恑傫偩屻丄恾嘦偺傛偆偵丄墿怓偲愒偺2曽岦偵恑傓偙偲偑弌棃傞偑丄偙傟傕惓廫擇柺懱偺懳徧惈偐傜峫偊偰丄偦偺屻偺宱楬偺屄悢偼摨偠偱偁傞丅 丂傛偭偰丄恾嘦偱倃偐傜惵愒偲恑傫偩屻偺宱楬傪俇攞偡傟偽傛偄偙偲偵側傞丅 丂傑偨丄惵愒偲恑傫偩傜丄墿怓偺慄偼捠傞偙偲偑弌棃側偄丅傛偭偰丄椢偺慄傪捠傜偹偽側傜側偄偙偲偵側傞丅 |
 |
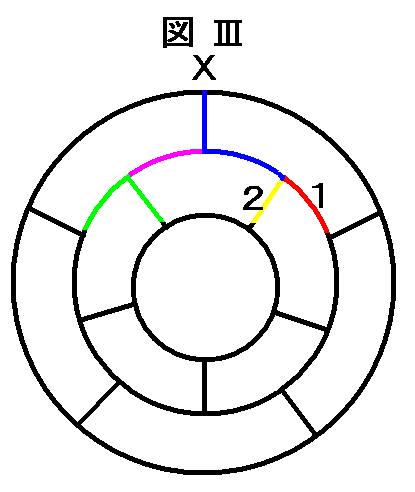
| 丂惵愒偲恑傫偩屻偼丄恾嘨偺傛偆偵丄宱楬侾偲俀偵暘偐傟傞丅偙偺俀偮偺宱楬偵偮偄偰偼丄懳徧惈偑側偄偲峫偊傜傟傞偺偱丄弴師峫偊偰偄偔偙偲偵偡傞丅師偺恾嘩偱偼丄婛偵慖偽傟偨宱楬偼惵偱揾傝丄崱偐傜慖傇傋偒宱楬偼愒偲墿偵揾偭偰偁傞丅傑偨丄婛偵慖偽傟偨宱楬偵傛傝捠傞偙偲偑弌棃側偔側偭偨慄偼奃怓偵丄捠傜偹偽側傜側偔惉偭偨慄偼椢偵揾傞丅 |  |
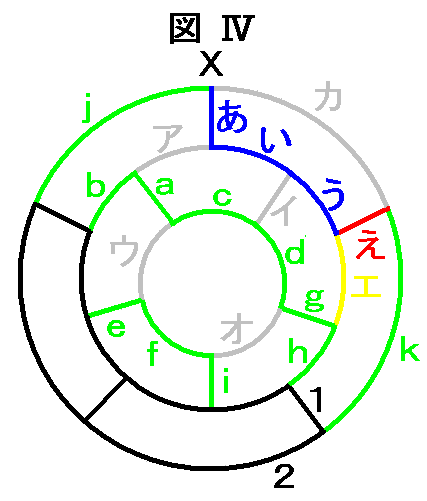
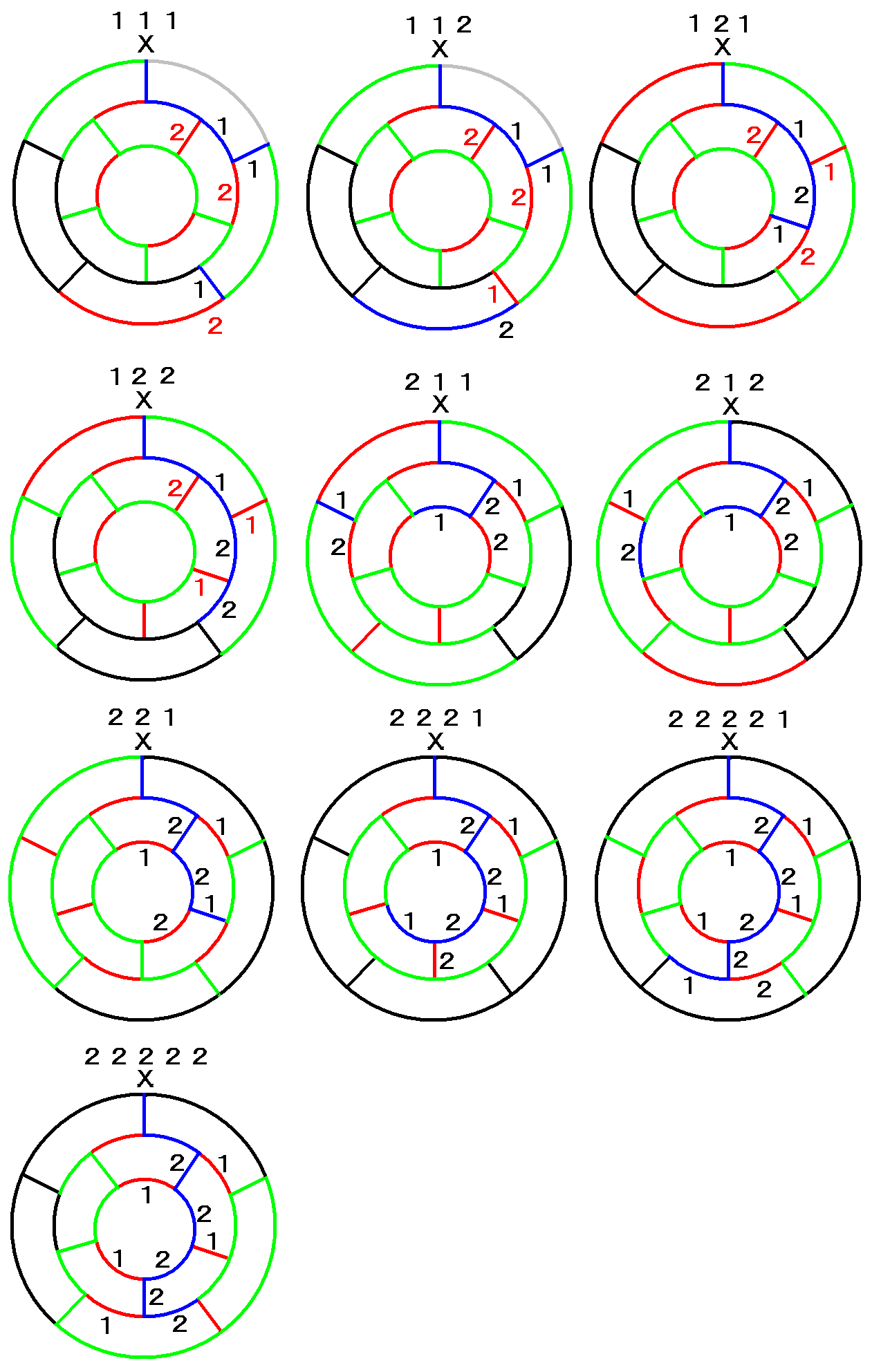
| 丂恾嘩傪梡偄偰宱楬偑偳偺傛偆偵寛掕偝傟傞偐傪愢柧偡傞丅恾嘩偼丄倃偐傜弌敪偟偰恾嘨偱偺惵慄傪捠傝峏偵侾傪慖戰偟偨偲偙傠偐傜巒傑傞丅偙偙偱丄恾嘩偺偊偐僄傪慖傇偙偲偵側傞偑丄偙偙偱偼偊傪慖傫偩傕偺偲偡傞丅傑偢偁偄傪捠偭偨偙偲偵傛傝傾偑捠傟側偔側傞丅偡傞偲丄倎倐傪捠傜側偗傟偽側傜側偔側傞丅師偵偄偆傪捠偭偨偙偲偵傛傝僀偑捠傟側偔側傞丅偡傞偲丄們倓傪捠傜側偗傟偽側傜側偔側傞丅倎們傪捠偭偨偙偲偵傛傝僂偑捠傟側偔側傞丅偡傞偲丄倕倖傪捠傜側偗傟偽側傜側偔側傞丅偆偊傪捠偭偨偙偲偵傛傝僄偑捠傟側偔側傞丅偡傞偲丄倗倛傪捠傜側偗傟偽側傜側偔側傞丅倓倗傪捠偭偨偙偲偵傛傝僆偑捠傟側偔側傞丅偡傞偲丄倝傪捠傜側偗傟偽側傜側偔側傞丅偊傪捠偭偨偙偲偵傛傝僇傪捠傞偲倃偵栠偭偰偟傑偆偺偱丄僇傪捠傟側偔側傞丅偡傞偲丄倞倠傪捠傜側偗傟偽側傜側偔側傞丅偙傟偱偁偄偆偊倠偲捠偭偰偒偰侾偲俀傪慖戰偡傞偙偲偵側偭偨偑丄偄偢傟傪慖戰偟偰傕丄侾捠傝偟偐宱楬偑柍偄偙偲偑尒偰庢傟傞偩傠偆丅侾傪慖戰偟偨応崌俁夞偺慖戰偱弴師侾侾侾偲慖傫偱宱楬偑寛掕偟丄俀傪慖戰偟偨応崌俁夞偺慖戰偱弴師侾侾俀偲慖傫偱宱楬偑寛掕偟偨偙偲偵側傞丅偙偺慖戰偺僷僞乕儞傪丄恾侾侾侾丆恾侾侾俀偺傛偆偵昞偟偰偄偔丅偨偩偟丄慖戰偑峴傢傟偰偄傞偲偙傠偵偼悢帤傪彂偒丄慖戰偟偨宱楬偼惵偱丄慖戰偝傟側偐偭偨慄偲寢壥偲偟偰捠傟側偔側偭偨慄傪愒偱丄捠傜偹偽側傜側偔側偭偨慄傪椢偱昞尰偡傞丅傑偨丄尒偨栚偱屻堦捠傝偟偐側偄偲暘偐傞偲偙傠傑偱傪昞尰偡傞丅 |  |
 |
|
丂侾侾侾偐傜俀俀俀俀俀傑偱偺10捠傝偑偁傞偺偱丄媮傔傞宱楬偺憤悢偼丄侾侽亊俇亖俇侽捠傝偱偁傞丅
丂俀侽侽俈擭搙偺怴擖惗偵丄忋恾傪梌偊偡傋偰偺宱楬傪尒偮偗偝偣偰傒偨偑丄俋捠傝傑偱偟偐尒偮偐傜傟側偐偭偨丅尦乆偺夝摎偼丄惓堦擇柺懱傪忋壓俀偮偵愗偭偰峀偘偰偄偨偺偱峏偵傗傗偙偟偐偭偨丅