２００６年日本数学オリンピック予選　問題１０

解答者　津山　竣太郎　２００７年６月

問題文

正十二面体のひとつの頂点Ｘをとる。一匹のアリがＸを出発し、正十二面体の辺上のみを歩き、Ｘ以外のすべての頂点をちょうど１度ずつ通過して、Ｘに戻ってきた。アリの歩いた経路として考えられるものは何通りあるか。ただし、回転で重なり合うような経路や、道順が逆になっただけの経路も、異なるものとして数える。

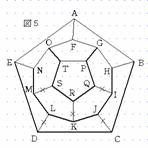
解答

　正十二面体のひとつの面に穴を開け、広げて平面状にすべての面を押し付ける。その際、各面の形はこの問題を考えるに際して関係ないので、右の図�Tのようであるとしてもよい。

次に五角形PQRSTと十角形FGHIJKLMNOを考える。例えば、OTを通ると、GP、IQ、KR、MSのうちいずれか１つを通らなければ、周囲（ABCDE）に戻れない（場合１）。また、外から中へ２回進むと、中から外へ２回進まなければ、周囲（ABCDE）に戻れない（場合２）。

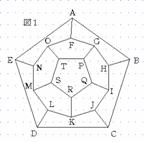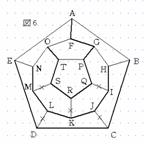
そこで、場合１について考える。まず、図２のようにOTとIQを通ることにすると、GPとKRとMSは通れないことになる。このとき、SとRを通るためには、TSRQと進まなければならない。同時に、Pを通るためにはTQRと進まなければならない。従って、OTとIQのような選び方は不適である。従って、2本の選び方は五角形PQRSTの隣り合う頂点を選びその頂点を含む2本を選ぶ方法しかない。この方法は５通りある。例えば、図３のようにOT、GPを選んだとすると、IQとKRとMSは通れないことになる。このとき、SとRとQを通るためには、図４のようにTSRQPを通らなければならない。さらに、IとKとMを通るためには、図４のようにHIJとJKLとLMNをとおらなければならない。

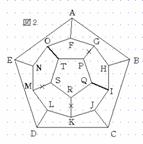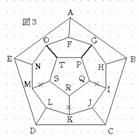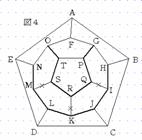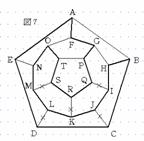
同様に、CJとDLは通れないことになるので、BCDとCDEを通らなければならない。また、GFOと通ることはできないので、AFは通らなければならない。次に、GFかOFのどちらかを通らなければならないので、ここでGFを通ることにする（図６）。すると、OFは通れないのでONを通ることになる。さらに、ENが通れなくなるので、EAを通ることになり、ABが通れないので、BHを通ることになる（図７）。これで経路が決定した。よって、この経路のとり方は、OTとGPのとり方が5通り、GFかOFのとり方が2通り、さらにA→Fと進むかF→Aと進むかの2通りあるので、５×２×２＝２０通りある。

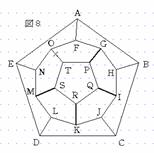
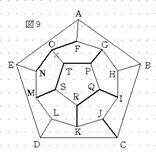
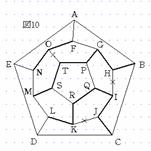
次に、場合２について考える。まず、5点P、Q、R、S、Tから4点選ぶ方法は5通りある。例えば、4点PQRSを選んだとする。すると、GP、IQ、KR、MSを通るので、OTは通れないことになる（図８）。従って、Tを通るためにはSTPを通らなければならない。するとQRも通らなければならない。また、Oを通るためにはFONを通らなければならない。さらに、IJKを通ることはできないので、Jを通るためにはCJを通らなければならない（図９）。次に、IJかKJのどちらかを通らなければならないので、ここでIJを通ることにする。すると、KJとIHは通れないので、KL、GH、HBを通ることになる（図10）。

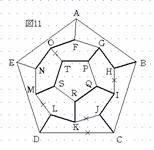
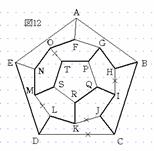
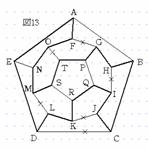
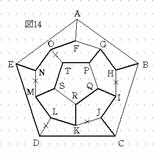
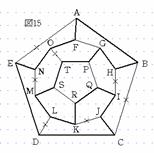
次に、DLかLMのどちらかを通らなければならないので、ここでDLを通ることにする（図11）。すると、CDとLMは通れないのでDE、CB、MNを通ることになる（図12）。従って、ABとFGは通れないので、AFとAEを通ることになり経路が確定する（図13）。また、LMを通ることにすると、DLとMNは通れないので、CDEとENを通らなければならない（図14）。従って、BCとAEが通れないので、BAFを通り経路が確定する（図15）。よって、この経路のとり方は、5点P、Q、R、S、Tから4点選ぶ方法が5通り、IJかKJのとり方が2通り、DLかLMのとり方が2通り、さらにA→Fと進むかF→Aと進むかの2通りあるので、５×２×２×２＝４０通りある。

以上より、総数は２０＋４０＝６０通りである。