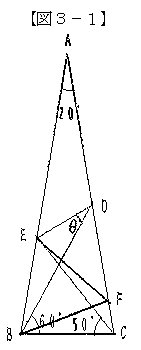乽嬼慠偺妏乿偺堦斒壔偵傓偗偰
亂擇摍曈嶰妏宍偐傜堦斒偺嶰妏宍偵亃
嫗搒嫵堢戝妛晬懏崅摍妛峑丂悢妛壢 彫戭丂朚晇
錗撪丂婤梇
侾丏偼偠傔偵
偐偹偰傛傝丄惗搆偐傜亂恾侾亅侾亃偺傛偆側擇摍曈嶰妏宍偺乽偁傞妏搙兤乿傪媮傔傞栤戣傪恞偹傜傟偙偲偑傛偔偁偭偨丅帡偐傛偭偰偼偄傞偑偄傠偄傠側栤戣偵弌夛偭偰偄偨丅
丂暯惉係擭搙嫗搒晎棫崅峑偺栤嶌埾堳傪偟偰偄傞愜傝丄埾堳夛偺媥宔帪偵嫵堢埾堳夛巜摫庡帠乮悢妛乯傛傝乽拞丒崅惗掱搙傪懳徾偵偟偨夝朄傪乿偲偺埶棅偑偁偭偨丅偦偺栤戣偼丄師偺亂恾侾亅俀亃偺傛偆側堦斒偺嶰妏宍傪懳徾偵偟偨栤戣嘥偱偁偭偨丅
栤戣嘥丂亂恾侾亅俀亃偺傛偆側嶰妏宍俙俛俠偵偍偄偰丄佢俢俛俠亖30亱丄佢俤俛俢亖50亱丄佢俛俠俤亖40亱丄佢俤C俢亖30亱偱偁傞偲偒丄佢俢俤俠偼壗搙偐丅
丂夝偒巒傔偰傒傞偲丄側偐側偐偺擄栤偱丄偦偺庡帠偐傜乽偙偺栤戣偵尷傜偢堦斒揑側夝朄偑偁傟偽乿偲偺埶棅傕偁傝丄摨椈偲憡択偟丄嫗搒嫵堢戝妛嶁壓廏抝柤梍嫵庼偺榑暥亀嬼慠偺妏亁偵偱偁偆偵帄偭偨丅
丂偙傟傪丄嶲峫偵偟偰屻弎俀丏偺夝朄偵偨偳傝拝偒丄摉帪榑暥偵傑偲傔偨丅壽戣偲偟偰丄摿偵屻敿偺埶棅偵摎偊傜傟傞傛偆偵偲巚峫偟偮偮10擭庛偺寧擔偑棳傟偨丅悢擭慜偵丄杮戝妛偱尰戙悢妛偺島媊傪扴摉偟偨偑丄偦偺嵺偵丄偙偺榑暥傪嫵嵽偲偟偰埖偭偨丅偦偟偰丄晄巚媍側偙偲偵丄栤戣嘥偲屻弎俁丏栤戣嘦偲偺娫偵丄幚偵婏嬾偱偁偭偨偑丄枾愙側丄偁傞娭學偑偁傞偙偲傪敪尒偟偨丅 |
 |
俀丏栤戣嘥偺夝朄偵偮偄偰
愭偢丄婎幉偲偟偰俠俤傪偲傜偊偰嶌恾偡傞丅
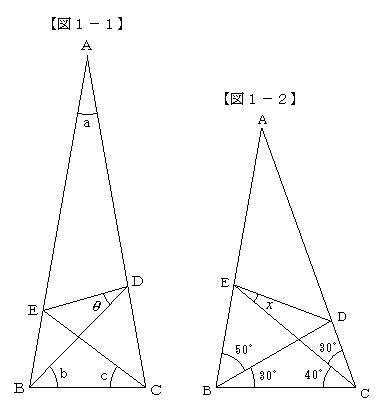
亂嶌恾亃壓偺亂恾俀亃偺傛偆偵丄乮1乯仮俠俤俛偲嵍塃懳徧側仮俤俠俧偺嶌惉丗丂佢俤俠俧亖60亱丄佢俠俤G亖40亱偲側傞揰G傪偲傝丄捈慄EG偲曈BC偲偺岎揰傪F偲偡傞丅
乮2乯惓嶰妏宍俥俠俫偺嶌惉丗丂佢CFH亖60亱丄佢FCH亖60亱偲側傞俫傪偲傞丅丂
亂夝亃仮俛俤俠偲仮俧俠俤偵偍偄偰丂EC亖CE乮嫟捠乯丆佢BEC亖佢GCE乮亖60亱乯丆佢BCE亖佢GEC乮亖40亱乯
備偊偵丄堦曈椉抂妏憡摍偵傛傝丄仮俛俤俠佭仮俧俠俤
傛偭偰丄俛俠亖俧俤丂乧嘆
乮1乯傛傝丄仮俥俠俤丄仮俤俛俥丆仮俠俥俧偼偄偢傟傕擇摍曈嶰妏宍
備偊偵丄俛俤亖俥俤亖俥俠亖俧俠丂乧嘇
乮2乯傛傝丄仮俥俠俫偼惓嶰妏宍丂丂備偊偵丄俥俠亖俠俫亖俫俥丂乧嘊
傛偭偰丄嘇丄嘊偵傛傝丄仮俠俫俧丄仮俥俫俤偼偦傟偧傟擇摍曈嶰妏宍
偟偨偑偭偰丄佢俤俧俫亖佢俤俧俠亅佢俫俧俠亖80亱乗50亱亖30亱
傑偨丄佢俫俤俧亖0丏5亊乮180亱亅佢俤俥俫乯亖0丏5亊乮180亱亅40亱乯亖70亱乧嘋
仮俛俠俢偲仮俧俤俫偵偍偄偰丄俛俠亖俧俤乮嘆傛傝乯
佢BCD亖佢GEH乮亖70亱乯丂丆丂佢DBC亖佢HGE乮亖30亱乯
備偊偵丄堦曈椉抂妏憡摍偵傛傝丄仮俛俠俢佭仮俧俤俫丂丂傛偭偰丄俠俢亖俤俫丂乧嘍
傑偨丄仮俢俤俠偲仮俫俠俤偵偍偄偰
俠俢亖俤俫乮嘍傛傝乯丂丂俤俠亖俠俤乮嫟捠乯丂
佢俢俠俤亖佢俫俤俠乮亖30亱乯
備偊偵丄擇曈汃妏憡摍偵傛傝丄仮俢俤俠佭仮俫俠俤
傛偭偰丄倶亖佢俢俤俠亖佢俫俠俤亖20亱 乮俻丏俤丏俢丏乯
丂偙偺夝偼丄拞丒崅惗搆偵棟夝偱偒傞偲偍傕傢傟傞偑丄彯丄堦斒壔偺壽戣偑巆偭偨丅偙偺壽戣崕暈偵岦偗偰偺娭傢傝偵偮偄偰偼丄屻弎偺係丏偵偍偄偰弎傋傞丅 |
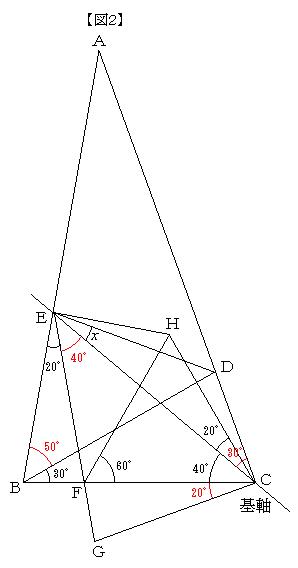 |
俁丏亀嬼慠偺妏亁偵偮偄偰偺徯夘偲専摙
嶁壓柤梍嫵庼偺榑暥偼丄撳崅峑丄搶戝帥崅峑偺擖帋傗嫗搒晎棫崅峑嫵堳嵦梡帋尡偵傕弌戣偝傟偰偄傞椶偺億僺儏儔乕側師偺傛偆側栤戣偐傜偼偠傑偭偰偄偨丅
栤戣嘦丂擇摍曈嶰妏宍俙俛俠乮俙俛亖俙俠乯
偵偍偄偰丄佢俛俙俠亖20亱丄佢俠俛俢亖60亱丄佢俛俠俤亖50亱偱偁傞偲偒丄佢俛俢俤偼壗搙偐丅
宖嵹偺夝
塃偺亂恾俁乗侾亃偺傛偆偵丄曈俙俠忋偵揰俥傪偲偭偰,佢俥俛俠亖20亱偱偁傞傛偆偵偲傞偲丄仮俤俛俠丄仮俥俛俠丆仮俢俛俥偼偦傟偧傟擇摍曈嶰妏宍偵側傞丅
偟偨偑偭偰丄俛俤亖俛俠亖俛俥亖俢俥
傑偨丄佢俤俛俥亖60亱丄俛俤亖俛俥偱偁傞偐傜仮俛俥俤偼惓嶰妏宍
備偊偵丄俛俥亖俥俤亖俤俛
傛偭偰丄仮俥俢俤傪峫偊傞偲
俥俤亖俥俢
佢俤俥俢亖180亱乗乮80亱亄60亱乯亖40亱傛傝丄
佢俤俢俥亖侽丏俆亊乮180亱亅佢EFD乯亖侽丏俆亊乮180亱亅40亱乯亖70亱
偟偨偑偭偰丄兤亖佢EDF乗佢BDF亖70亱亅40亱亖30亱
乮俻丏俤丏俢丏乯
幚偵丄僗儅乕僩側偲偰傕旤偟偄夝偱偁傞丅
偙傟偼丄1922擭10寧偵塸崙偺The mathematical
gazette偲偄偆嶨帍偵俵丏Laugley巵偑採帵偟丄偙傟傪堦斒壔偟偨傕偺傪1975擭6寧偵Colin
Tripp巵偑採帵偟偰偄傞丅
偙傟偵傛傞偲丄亂恾3乗俀亃偺傛偆偵倎乮佢A乯丄倐乮佢CBD乯,們乮佢BCE乯偑梌偊傜傟傞偲兤乮佢BDE乯偑寛傑傞偑丄拞妛峑偱曌嫮偟偰偒偨弶摍婔壗妛偱媮傑傞偐偲偄偆偲丄偦傟偼傓偮偐偟偔丄崅摍悢妛偺暋慺夝愅妛偑昁梫偲側傞丅乮a丄倐丄們偑惍悢偱偁偭偰傕兤偑惍悢搙偲側傞偙偲偼傑傟偱偁傞丅乯
Colin Tripp巵偑僐儞僺儏乕僞偵丄偙傟傜偑惍悢偵側傞偲偒偺妏搙傪寁嶼偝偣偨偲偙傠丄師偺昞偺53捠傝偑偱偰偒偨偲徯夘偝傟偰偄傞丅
|
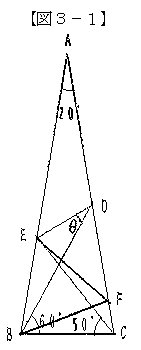 |
| 亂堦棗昞侾亃丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂扨埵偼搙亃(幬懱偺悢帤偼栤戣嘦) |
| a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
| 4 |
46 |
4 |
2 |
丂 |
4 |
46 |
44 |
42 |
丂 |
12 |
72 |
42 |
6 |
丂 |
12 |
72 |
66 |
30 |
丂 |
28 |
52 |
28 |
14 |
丂 |
28 |
52 |
38 |
24 |
丂 |
56 |
59 |
31 |
3 |
丂 |
56 |
59 |
56 |
28 |
| 8 |
47 |
8 |
4 |
丂 |
8 |
47 |
43 |
39 |
丂 |
16 |
49 |
16 |
8 |
丂 |
16 |
49 |
41 |
33 |
丂 |
32 |
53 |
32 |
16 |
丂 |
32 |
53 |
37 |
21 |
丂 |
72 |
39 |
21 |
12 |
丂 |
72 |
39 |
27 |
18 |
| 12 |
42 |
18 |
12 |
丂 |
12 |
42 |
30 |
24 |
丂 |
20 |
50 |
20 |
10 |
丂 |
20 |
50 |
40 |
30 |
丂 |
36 |
54 |
36 |
18 |
丂 |
|
|
|
|
丂 |
72 |
42 |
24 |
12 |
丂 |
72 |
42 |
39 |
18 |
| 12 |
48 |
12 |
6 |
丂 |
12 |
48 |
42 |
36 |
丂 |
20 |
60 |
30 |
10 |
丂 |
20 |
60 |
50 |
30 |
丂 |
40 |
55 |
35 |
15 |
丂 |
40 |
55 |
40 |
20 |
丂 |
72 |
48 |
24 |
6 |
丂 |
72 |
48 |
42 |
24 |
| 12 |
57 |
33 |
15 |
丂 |
12 |
57 |
42 |
24 |
丂 |
20 |
65 |
25 |
5 |
丂 |
20 |
65 |
60 |
40 |
丂 |
44 |
56 |
34 |
12 |
丂 |
44 |
56 |
44 |
22 |
丂 |
72 |
51 |
39 |
9 |
丂 |
72 |
51 |
42 |
12 |
| 12 |
66 |
42 |
12 |
丂 |
12 |
66 |
54 |
24 |
丂 |
20 |
70 |
50 |
10 |
丂 |
20 |
70 |
60 |
20 |
丂 |
48 |
57 |
33 |
9 |
丂 |
48 |
57 |
48 |
24 |
丂 |
120 |
24 |
12 |
6 |
丂 |
120 |
24 |
18 |
12 |
| 12 |
69 |
21 |
3 |
丂 |
12 |
69 |
66 |
48 |
丂 |
24 |
51 |
24 |
12 |
丂 |
24 |
51 |
39 |
27 |
丂 |
52 |
58 |
32 |
6 |
丂 |
52 |
58 |
52 |
26 |
丂 |
|
|
|
|
|
|
|
|
丂 |
忋婰偺傛偆側棟憐揑側徹柧偱偼側偄偑丄栤戣嘦偵偨偄偟偰丄巹偺暿夝傪採帵偟丄側偵偐嫟捠揰偑偁傞偺偐傪挷傋偰傒傞丅
亂恾俁亅俁亃偺傛偆偵丄揰俥傪仮俥俛俠偑惓嶰妏宍偲側傞傛偆偵偲傞丅丂乧嘆
俠俥偺墑挿偲慄暘俙俛偲偺岎揰傪俧偲偡傞偲丄仮俥俢俧偼惓嶰妏宍偱偁傞偙偲傪帵偡丅
佢俢俥俧亖佢俛俥俠乮懳捀妏乯亖60亱丂乧嘇
傑偨丄仮俛俥俧偲仮俠俥俢偵偍偄偰
俛俥亖俠俥乮惓嶰妏宍偺曈乯丂佢俧俛俥亖佢俢俠俥乮亖20亱乯
佢俛俥俧亖佢俠俥俢乮亖120亱乯
備偊偵丄堦曈椉抂妏憡摍偵傛傝丄
仮俛俥俧佭仮俠俥俢
傛偭偰丄俥俧亖俥俢丂乧嘊
偟偨偑偭偰丄嘇丆嘊偵傛傝丄仮俥俢俧偼惓嶰宍偱偁傞偲偄偊傞丅
備偊偵丄俥俢亖俢俧亖俧俥丂乧嘋
傑偨丄佢俛俠俤亖佢俛俤俠乮亖50亱乯傛傝丄仮俛俠俤偼擇摍曈嶰妏宍
備偊偵丄俛俠亖俛俤丂乧嘍
嘆傛 傝丄俛俠亖俛俥丂乧嘐
嘍丄嘐偵傛傝丄仮俛俥俤偼擇摍曈嶰妏宍
傛偭偰丄佢俛俥俤亖佢俛俤俥乮亖80亱乯
偟偨偑偭偰丄佢俤俥俧亖佢俛俥俧亅佢俛俥俤亖40亱丂乧嘑
堦曽丄仮俛俠俧偵偍偄偰丄佢俠俧俛亖180亱乗乮佢俧俛俠亄佢俛俠俧乯亖40亱丂乧嘒
嘑丄嘒偵傛傝丄仮俤俥俧偼擇摍曈嶰妏宍
備偊偵丄俤俥亖俤俧丂乧嘓
仮俤俥俢偲仮俤俧俢偵偍偄偰
嘓傛傝丄俤俥亖俤俧丂丂嘋傛傝丄俥俢亖俧俢丂丂傑偨丄俤俢亖俤俢乮嫟捠乯
備偊偵丄嶰曈憡摍偵傛傝丄仮俤俥俢佭仮俤俧俢
傛偭偰丄佢俥俢俤亖佢俧俢俤亖0.5亊佢俥俢俧亖0.5亊60亱
偟偨偑偭偰丄佢俛俢俤亖30亱丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俻丏俤丏俢丏乯 |
 |
栤戣嘦偵娭偟偰偼丄偙偺夝偲俁丏偺旤偟偄夝偲斾妑偡傞偲偒丄僗儅乕僩偝偵嵎偼偁傞偑丄嫟捠揰偲偟偰偼丄惓嶰妏宍偲擇摍曈嶰妏宍偵夝朄偺僉乕偑偁傞偲偍傕傢傟傞偙偲偱偁傞丅
偙傟傜偑尰傟傞弴彉偵堘偄偼偁傞偑丄偨偲偊丄僞僀儈儞僌偺堘偄偑偁偭偰傕丄偙傟傜傪昁梫偲偟偰偄傞偙偲偵偼偐傢傝側偄丅
偙偺偙偲偵傛傝丄拞丒崅惗搆偵傛傞懡條側夝偑婜懸偱偒傞丅
係丏乽拞妛丒崅峑惗傪懳徾偵偟偨怴偨側夝朄乿傊偺峫嶡
| 栤戣嘦丂擇摍曈嶰妏宍俙俛俠乮俙俛亖俙俠乯偵偍偄偰丄佢俛俙俠亖20亱丄佢俠俛俢亖60亱丄佢俛俠俤亖50亱偱偁傞偲偒丄佢俛俢俤偼壗搙偐丅 |
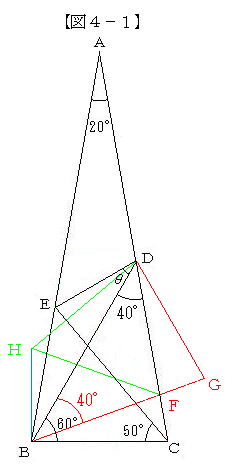 |
| 師偄偱丄栤戣嘥偺慜弎俀丏偵偍偗傞夝朄偵増偭偰忋偺栤戣嘦偺夝傪峫偊丄栤戣侾偺堦斒壔偵挧愴偟偰傒偨丅 |
乮夝乯俀丏偺夝朄偲慡偔摨條偺庤弴偱丄崱夞偼丄婎幉偲偟偰俛俢傪偲傝亂恾係乗1亃偺傛偆偵嶌恾偡傞丅
亂嶌恾亃乮侾乯仮俛俢俠偲嵍塃懳徧側仮俢俛俧偺嶌惉丗丂佢俛俢俧亖60亱丄佢俢俛俧亖40亱偱偁傞揰俧傪偲傝丆慄暘BG偲慄暘俙俠偲偺岎揰傪俥偲偡傞丅
乮俀乯惓嶰妏宍俥俢俫偺嶌惉丗丂佢俥俢俫亖60亱丄佢俢俥俫亖60亱偱偁傞揰俫傪偲傞丅
亂夝亃嶌恾偵傛傝丄慜弎偺俀丏偺夝朄庤弴偲慡偔摨條偵偟偰丄擇曈汃妏憡摍偵傛傝丂丂仮俢俛俤佭仮俛俢俫
偙偺屻傕摨條偵偟偰丄兤亖佢俢俛俫亖30亱傪摼傞丅
乮俻丏俤丏俢丏乯
拞妛惗彅孨偼丄塃偺恾偺拞偵俀摍曈嶰妏宍偑偨偔偝傫偁傞偙偲傪妋擣偟偰偔偩偝偄丅 |
偙傟傛傝丄栤戣嘥偲栤戣嘦偺夝朄偺嫟捠揰偲側傞億僀儞僩偼婎幉愝掕偵偁傝丄師偄偱丄嵍塃懳徧側嶰妏宍丄惓嶰妏宍丄擇摍曈嶰妏宍偺妶梡偵偁傞丅
俆丏怴偨側夝朄偺敪尒
偝偰丄婏嬾偵傕栤戣嘥偲栤戣嘦偲偵枾愙側學傢傝偑偁傝丄偙偺捈愙揑側娭楢傪梡偄偨怴偨側夝朄偵偮偄偰弎傋傞丅乮偨偩偟丄嶰妏宍乮俙俛俠乯偼嶰妏宍乮俙乯乮俛乯乮俠乯偺偙偲傪帵偡傕偺偲偡傞乯
| 栤戣嘥丂嶰妏宍(俙俛俠)偵偍偄偰丄佢(俢俛俠)亖30亱丄佢(俤俛俢)亖50亱丄佢(俛俠俤)亖40亱丄佢(俤C俢)亖30亱偱偁傞偲偒丄佢(俢俤俠)偼壗搙偐丅 |
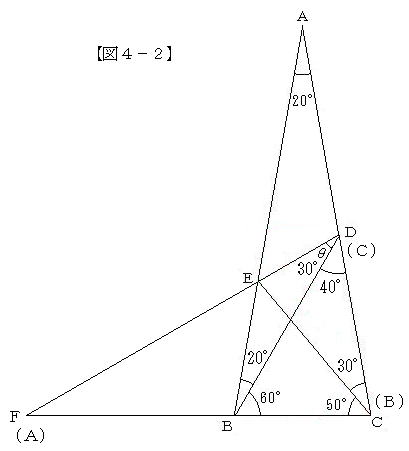 |
乮敪尒偟偨夝乯亂恾4乕俀亃偺傛偆偵丄栤戣嘦偺擇摍曈嶰妏宍ABC偵偍偄偰丄2捈慄俢俤偲俠俛偺岎揰傪俥偲偡傞丅
栤戣嘦夝朄偺寢壥兤亖30亱偱偁傞偙偲傛傝
佢俥俠俢亖佢俥俠俤亄佢俤俠俢亖50亱亄30亱亖80亱
佢俥俢俠亖佢俥俢俛亄佢俛俢俠亖30亱+40亱亖70亱
備偊偵丄佢俠俥俢亖180亱亅乮佢俥俠俢亄佢俥俢俠乯亖30亱
傛偭偰丄仮俥俠俢偼亂恾係亅2亃偺傛偆偵仮乮俙俛俠乯偲摨偠傕偺偱偁傞偙偲傛傝
佢俤俛俢亖佢乮俢俤俠乯
偟偨偑偭偰丄佢(俢俤俠)亖20亱乮俻丏俤丏俢丏乯 |
傑偝偵丄亂擇摍曈嶰妏宍偐傜堦斒偺嶰妏宍偵亃偑幚尰偝傟偰偄傞偲偄偊傞丅
偙偺傛偆偵偟偰丄擇摍曈嶰妏宍傪懳徾偵偟偨5俁庬慡偰偵娭偟偰丄堦斒偺嶰妏宍偵墳梡丄偱偒傞偲偄偊傞丅
俆丏乽栤戣嘥傪娷傔偨堦斒揑側夝朄乿偺傑偲傔偵偮偄偰
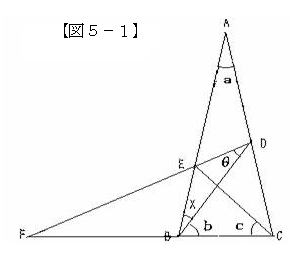
慜婰俁丏偵宖偘偨堦棗昞偵偁傞53捠傝偺擇摍曈嶰妏宍偺(倎丄倐丄們丄兤乯傪媮傔傞偙偲偑偱偒傞偙偲傛傝丄亂恾5乗侾亃偺2捈慄俠俛偲俢俤偺岎揰傪俥偲偡傞偲丄偙傟偵懳墳偡傞堦斒偺嶰妏宍俥俠俢偵偍偗傞嬼慠偺妏倶傪摿掕偡傞偙偲偑偱偒傞丅偙傟偲慡偔摨條偵偟偰53庬偺堦斒偺嶰妏宍偵偍偗傞乽嬼慠偺妏乿傪堦棗昞偺惍悢乮倶乯偺傛偆偵媮傔傞偙偲偑偱偒傞丅
倶亖0.5亊乮180亱亅 a乯乗倐丂偵傛傝丄倶偼師偺亂堦棗昞俀亃偺傛偆偵側傞丅 |
 |
| 亂堦棗昞2亃丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(幬懱偺悢帤偼栤戣嘦)丂丂亂扨埵偼搙亃 |
| a |
倐 |
們 |
兤 |
x |
丂 |
x |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
x |
丂 |
x |
a |
倐 |
們 |
兤 |
丂 |
a |
倐 |
們 |
兤 |
x |
丂 |
x |
a |
倐 |
們 |
兤 |
| 4 |
46 |
4 |
2 |
42 |
丂 |
42 |
4 |
46 |
44 |
42 |
|
20 |
50 |
20 |
10 |
30 |
丂 |
30 |
20 |
50 |
40 |
30 |
丂 |
44 |
56 |
34 |
12 |
12 |
丂 |
12 |
44 |
56 |
44 |
22 |
| 8 |
47 |
8 |
4 |
39 |
丂 |
39 |
8 |
47 |
43 |
39 |
|
20 |
60 |
30 |
10 |
20 |
丂 |
20 |
20 |
60 |
50 |
30 |
丂 |
48 |
57 |
33 |
9 |
9 |
丂 |
9 |
48 |
57 |
48 |
24 |
| 12 |
42 |
18 |
12 |
42 |
丂 |
42 |
12 |
42 |
30 |
24 |
|
20 |
65 |
25 |
5 |
15 |
丂 |
15 |
20 |
65 |
60 |
40 |
丂 |
52 |
58 |
32 |
6 |
6 |
丂 |
6 |
52 |
58 |
52 |
26 |
| 12 |
48 |
12 |
6 |
36 |
丂 |
36 |
12 |
48 |
42 |
36 |
|
20 |
70 |
50 |
10 |
10 |
丂 |
10 |
20 |
70 |
60 |
20 |
丂 |
56 |
59 |
31 |
3 |
3 |
丂 |
3 |
56 |
59 |
56 |
28 |
| 12 |
57 |
33 |
15 |
27 |
丂 |
27 |
12 |
57 |
42 |
24 |
|
24 |
51 |
24 |
12 |
27 |
丂 |
27 |
24 |
51 |
39 |
27 |
丂 |
72 |
39 |
21 |
12 |
15 |
丂 |
15 |
72 |
39 |
27 |
18 |
| 12 |
66 |
42 |
12 |
18 |
丂 |
18 |
12 |
66 |
54 |
24 |
|
28 |
52 |
28 |
14 |
24 |
丂 |
24 |
28 |
52 |
38 |
24 |
|
72 |
42 |
24 |
12 |
12 |
丂 |
12 |
72 |
42 |
39 |
18 |
| 12 |
69 |
21 |
3 |
15 |
丂 |
15 |
12 |
69 |
66 |
48 |
|
32 |
53 |
32 |
16 |
21 |
丂 |
21 |
32 |
53 |
37 |
21 |
|
72 |
48 |
24 |
6 |
6 |
丂 |
6 |
72 |
48 |
42 |
24 |
| 12 |
72 |
42 |
6 |
12 |
丂 |
12 |
12 |
72 |
66 |
30 |
丂 |
36 |
54 |
36 |
18 |
18 |
丂 |
|
|
|
|
|
|
72 |
51 |
39 |
9 |
3 |
丂 |
3 |
72 |
51 |
42 |
12 |
| 16 |
49 |
16 |
8 |
33 |
丂 |
33 |
16 |
49 |
41 |
33 |
丂 |
40 |
55 |
35 |
15 |
15 |
丂 |
15 |
40 |
55 |
40 |
20 |
|
120 |
24 |
12 |
6 |
6 |
丂 |
6 |
120 |
24 |
18 |
12 |
扥屻嫵庼偺榑暥偵丄奺堦棗昞偺嵍塃懳徠(倎丄倐丄們丄兤乯丗乮a丄倐丄倐乗兤丄倐乗們乯偺徯夘偑偁傞
偄偢傟偺倶傕摍偟偄偙偲偑柺敀偄丅
俙俛亖俙俠丄捀妏倎偺擇摍曈嶰妏宍俙俛俠傪峫偊傞丅
佢俢俛俠亖倐丄佢俤俠俛亖們丄佢俤俢俛亖兤偲偡傞丅
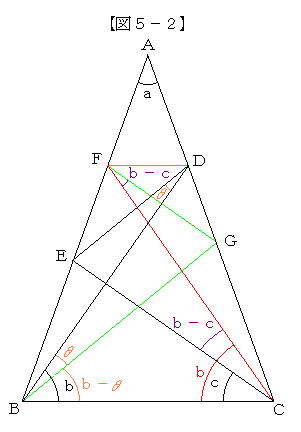
亂恾俆亅俀亃偺傛偆偵丄俥俢偲俛俠丄俤俢偲俛俧偑偦傟偧傟暯峴偲側傞俥丆俧傪曈俙俛丆俙俠忋偵偲傞丅
偙偙偱丄嶰妏宍偵偍偗傞暯峴慄偲斾偺惈幙傪梡偄傞偲俥俧偲俤俠偑暯峴偲偄偊傞丅
俁慻偺暯峴慄偺嶖妏偼偦傟偧傟摍偟偄偺偱丄俙俛亖俙俠傪壛枴偟偰丄佢俥俠俛亖倐丆佢俢俛俧亖兤傛傝丄
佢俧俛俠亖倐乗兤
佢俥俠俤亖倐亅們傛傝佢俧俥俠亖倐亅們
偝傜偵丄倐亅兤亙倐傛傝嶰妏宍俙俛俠傪嵍塃偵棤曉偡偲乮倎丆倐丄倐亅兤丄倐亅們乯傪摼傞丅 |
 |
偝偰丄53捠傝偺擇摍曈嶰妏宍偵懳偟偰丄乽嬼慠偺妏乿偱偁傞惍悢兤偑懚嵼偡傞丅
偦傟偵壛偊偰丄偦傟傜偐傜摫偐傟傞53捠傝偺堦斒偺嶰妏宍偵懳偟偰丄乽嬼慠偺妏乿偱偁傞惍悢倶偑媮傔傜傟傞偙偲傪徯夘偟偨丅
偟偐偟丄堦斒偺嶰妏宍偺側偐偵偼丄擇摍曈嶰妏宍偵側傞傕偺偑侾係捠傝乮亂堦棗昞俀亃偺愒帤偺悢帤乯偁傞丅
傛偭偰丄幚嵺偵偼摫偐傟傞傕偺偼39捠傝懚嵼偡傞丅
塃偺亂堦棗昞俁亃偼偦傟傜傪楍嫇偟偨傕偺偱偁傞丅
丂偨偩偟丄亂恾俆亅侾亃偺嶰妏宍俥俠俢傪嶰妏宍乮俙俛俠乯偵尒棫偰傞偲丄師偺傛偆偱偁傞丅
佢乮俛俙俠乯亖佢俢俛俠乗佢俤俢俛
丂亪丂倎丂丂亖丂倐亅兤
佢乮俠俛俢乯亖佢俙俠俛亅佢俤俠俛
丂亪丂倐丂丂亖乮90亱乗倎/俀乯乗們
佢乮俛俠俤乯亖佢俛俙俢+佢俙俛俢亖倎+倶丂
丂亪丂們丂丂亖倎+乮90亱乗倎/俀乯乗倐
俙亖倎丂亖丂倐亅兤
俛亖佢俙俠俛亖90亱乗倎/俀
俠亖佢俤俢俛+佢俛俢俠亖兤+90亱亄倎/俀乗倐 |
亂堦棗昞俁亃 |
| 堦斒偺嶰妏宍 |
杮偵側傞
俀摍曈嶰妏宍 |
丂 |
堦斒偺嶰妏宍 |
杮偵側傞
俀摍曈嶰妏宍 |
丂 |
堦斒偺嶰妏宍 |
杮偵側傞
俀摍曈嶰妏宍 |
| 俙 |
俛 |
俠 |
倐 |
們 |
x |
a |
倐 |
們 |
兤 |
丂 |
俙 |
俛 |
俠 |
倐 |
們 |
x |
a |
倐 |
們 |
兤 |
丂 |
俙 |
俛 |
俠 |
倐 |
們 |
x |
a |
倐 |
們 |
兤 |
| 44 |
88 |
48 |
84 |
46 |
42 |
4 |
46 |
4 |
2 |
丂 |
41 |
82 |
57 |
66 |
49 |
33 |
16 |
49 |
16 |
8 |
丂 |
33 |
66 |
81 |
18 |
57 |
9 |
48 |
57 |
48 |
24 |
| 43 |
86 |
51 |
78 |
47 |
39 |
8 |
47 |
8 |
4 |
丂 |
60 |
80 |
40 |
55 |
35 |
15 |
20 |
65 |
25 |
5 |
丂 |
32 |
64 |
84 |
12 |
58 |
6 |
52 |
58 |
52 |
26 |
| 66 |
84 |
30 |
63 |
27 |
15 |
12 |
69 |
21 |
3 |
丂 |
60 |
80 |
40 |
30 |
30 |
10 |
20 |
70 |
50 |
10 |
丂 |
31 |
62 |
87 |
6 |
59 |
3 |
56 |
59 |
56 |
28 |
| 66 |
84 |
30 |
42 |
24 |
12 |
12 |
72 |
42 |
6 |
丂 |
50 |
80 |
50 |
50 |
40 |
20 |
20 |
60 |
30 |
10 |
丂 |
42 |
54 |
84 |
30 |
78 |
6 |
72 |
48 |
24 |
6 |
| 42 |
84 |
54 |
72 |
48 |
36 |
12 |
48 |
12 |
6 |
丂 |
40 |
80 |
60 |
60 |
50 |
30 |
20 |
50 |
20 |
10 |
丂 |
42 |
54 |
84 |
15 |
75 |
3 |
72 |
51 |
39 |
9 |
| 54 |
84 |
42 |
42 |
30 |
18 |
12 |
66 |
42 |
12 |
丂 |
50 |
80 |
50 |
20 |
30 |
10 |
20 |
70 |
60 |
20 |
丂 |
30 |
54 |
96 |
30 |
84 |
12 |
72 |
42 |
24 |
12 |
| 30 |
84 |
66 |
66 |
54 |
42 |
12 |
42 |
18 |
12 |
丂 |
30 |
80 |
70 |
30 |
40 |
20 |
20 |
60 |
50 |
30 |
丂 |
27 |
54 |
99 |
33 |
87 |
15 |
72 |
39 |
21 |
12 |
| 42 |
84 |
54 |
51 |
39 |
27 |
12 |
57 |
33 |
15 |
丂 |
25 |
80 |
75 |
20 |
35 |
15 |
20 |
65 |
60 |
40 |
丂 |
39 |
54 |
87 |
12 |
75 |
3 |
72 |
51 |
42 |
12 |
| 42 |
84 |
54 |
30 |
30 |
18 |
12 |
66 |
54 |
24 |
丂 |
39 |
78 |
63 |
54 |
51 |
27 |
24 |
51 |
24 |
12 |
丂 |
24 |
54 |
102 |
15 |
84 |
12 |
72 |
42 |
39 |
18 |
| 33 |
84 |
63 |
42 |
39 |
27 |
12 |
57 |
42 |
24 |
丂 |
38 |
76 |
66 |
48 |
52 |
24 |
28 |
52 |
28 |
14 |
丂 |
21 |
54 |
105 |
27 |
87 |
15 |
72 |
39 |
27 |
18 |
| 18 |
84 |
78 |
54 |
54 |
42 |
12 |
42 |
30 |
24 |
丂 |
37 |
74 |
69 |
42 |
53 |
21 |
32 |
53 |
32 |
16 |
丂 |
24 |
54 |
102 |
12 |
78 |
6 |
72 |
48 |
42 |
24 |
| 42 |
84 |
54 |
18 |
24 |
12 |
12 |
72 |
66 |
30 |
|
35 |
70 |
75 |
30 |
55 |
15 |
40 |
55 |
40 |
20 |
丂 |
18 |
30 |
132 |
18 |
126 |
6 |
120 |
24 |
12 |
6 |
| 21 |
84 |
75 |
18 |
27 |
15 |
12 |
69 |
66 |
48 |
丂 |
34 |
68 |
78 |
24 |
56 |
12 |
44 |
56 |
44 |
22 |
丂 |
12 |
30 |
138 |
12 |
126 |
6 |
120 |
24 |
18 |
12 |
俇丏崱屻偺壽戣
傑偨丄惍悢偺榞傪偼偢偣偽丄僕儍僶傪梡偄偰丄柍悢偺乽嬼慠偺妏乿偱偁傞幚悢兤偲幚悢倶偺娭學傪塃偺恾偺傛偆偵尒傞偙偲偑偱偒傞丅崱屻偼偙偺僕儍僶傪帺桼偵庢傝埖偊傞傛偆偵媄弍傪廗摼偟丄堦憌偙偺尋媶傪怺傔偰丄偦偺偲傝傑偲傔偵偮偲傔偰偄偒偨偄丅
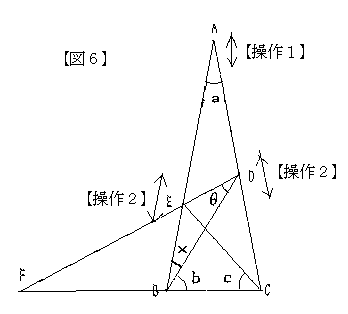
僕儍僶偵傛傞亂憖嶌侾亃忋偺亂恾俇亃偵偍偄偰丄擇摍曈嶰妏宍俙俛俠偺捀揰俙傪丄掙曈偲悅捈曽岦偵忋壓堏摦偡傞偙偲偵傛傝丄偁傜備傞擇摍曈嶰妏宍傪懳徾偵偡傞偙偲偑偱偒傞丅
亂憖嶌俀亃堎側傞摍曈忋偺俀揰俢丆俤傪偦傟偧傟偺曈忋偵増偭偰堏摦偡傞偙偲偵傛傝丄堦斒偺嶰妏宍傪懳徾偵偡傞偙偲偑偱偒傞丅
埲忋偺憖嶌偵傛傝丄乮a丄倐丄們丄兤乯偑楢摦偟偰曄壔偟寛掕偡傞丅傑偨丄偦傟偵敽偭偰倶偑曄壔偟寛掕偡傞丅
忋婰偺亂憖嶌侾亃丄亂憖嶌俀亃偺堄枴偼丄嫗搒嫵堢戝妛扥屻嫵庼偺亀扥屻偺儁乕僕亁乮http://homepage2.nifty.com/tangoh/)偺恾宍偵娭偡傞徹柧偺拞偱巊傢傟偰偄傞儃僞儞偵傛傞恾宍曄宍偺偙偲偱偡丅嫽枴傪偍帩偪偺曽偼丄偦偪傜傕偛棗壓偝偄丅 |
 |
俈丏偍傢傝偵
丂嵟屻偵丄嫗搒嫵堢戝妛扥屻嫵庼偺亀扥屻偺儁乕僕亁傪徯夘偟偰偍偒偨偄丅嶁壓柤梍嫵庼偺亀嬼慠偺妏亁偼弶摍婔壗妛傪梡偄偨徹柧丒峫嶡偱偁傝丄扥屻嫵庼偺乽嬼慠偺妏搙乿偼丄弶摍婔壗妛丄嶰妏娭悢偵傛傞徹柧傪娷傒丄偝傜偵偼崅摍悢妛傪嬱巊偟偨慜弎偺俆俁捠傝慡偰偺徹柧偱偁傞丅
丂偙傟偼丄暋慺悢傪梡偄丄偄偔偮偐偺掕棟傪揥奐偟偰丄偦偺夝朄傪弎傋偨傕偺偱偁傞丏
丂嫵庼偺儂乕儉儁乕僕偵偼丄嫽枴怺偄傕偺偑偨偔偝傫徯夘偝傟偰偄傞丏偙傟偵娭怱傪婑偣傜傟傞愭惗曽偼丄惀旕丄扥屻嫵庼偺壓婰儂乕儉儁乕僕亀扥屻偺儁乕僕亁傪偛棗偄偨偩偒偨偄丅
亀扥屻偺儁乕僕亁儂乕儉儁乕僕愭
丂丂http://homepage2.nifty.com/tangoh/
亂嶲峫暥專亃
侾丏嫗搒嫵堢戝妛嶁壓柤梍嫵庼榑暥丗亀嬼慠偺妏亁
俀丏嫗搒嫵堢戝妛扥屻嫵庼榑暥丗暋慺悢偲弶摍婔壗俠倛倎倫倲倕倰俁丏扨埵墌偺婔壗妛乽嬼慠偺妏搙乿
偦偺懠
亂嫤椡偟偰偄偨偩偄偨愭惗曽亃
嫗搒嫵堢戝妛嫵庼丂丂丂丂丂扥屻丂峅巌巵
嫗搒晎棫崅摍妛峑峑挿丂丂丂彑娫丂婌堦榊巵
嫗搒晎棫崅摍妛峑嫵桜丂丂丂扟杮丂媊榓巵
嫗搒晎棫崅摍妛峑嫵桜丂丂丂愇堜丂搘巵
嫗搒嫵堢戝妛晬懏崅摍妛峑丂壨嶈丂揘巏巵